武警警官学院基础部 四川成都 610213
摘要:在学习重积分时,利用轮换对称是一种计算简便且效率很高的方法,本文对轮换对称性在多元函数微积分学中用法进行探索、追溯和总结。
关键字:轮换对称 应用
轮换对称的概念
如果一个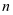 元代数式
元代数式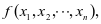 如果将字母
如果将字母 以
以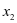 代替
代替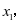
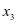 代替
代替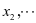
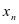 代替
代替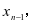
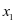 代替
代替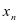 后表达式不发生改变,即
后表达式不发生改变,即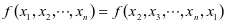 ,那么称这个代数为
,那么称这个代数为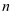 元轮换对称式,简称轮换式,例如
元轮换对称式,简称轮换式,例如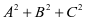 显然是轮换对称式。
显然是轮换对称式。
轮换对称的雏形
在《高等数学》讲解旋转曲面的内容,例如,旋转抛物面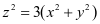 是由
是由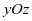 坐标面上直线
坐标面上直线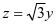 绕
绕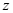 轴旋转而来。我们来观察这张二次曲面方程形式,自变量
轴旋转而来。我们来观察这张二次曲面方程形式,自变量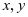 形式是完全相同的,我认为这是轮换对称的雏形。
形式是完全相同的,我认为这是轮换对称的雏形。
应用
接下来我们通过例题,将轮换对称性在多元函数微积分学中的简化运算和应用进行简单举例说明。
3.1求偏导数
例 1 设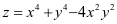 ,求
,求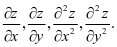
解 由于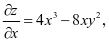 而函数
而函数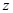 关于变量
关于变量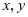 具有轮换对称性,则
具有轮换对称性,则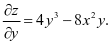
由于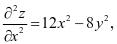 同理可得
同理可得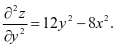
本题在求偏导数时,利用两个自变量的轮换对称性,将变量进行替换,运算量减半。
3.2 求极值
多元函数求条件极值时,当表达式达到轮换对称性时,函数取相应的极值。
例2 将12分成三个正整数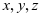 之和,使得
之和,使得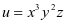 为最大。
为最大。
解 令拉格朗日函数
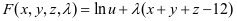
即
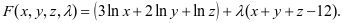
则分别求四个一阶偏导数:
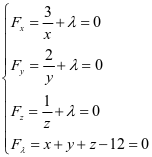
解得唯一驻点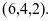 故最大值为
故最大值为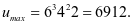
本题中采用了求条件极值一贯的思路,未展示求到驻点的过程。不过只有上述部分,观察轮换对称性足够了。很多学生开始认为变量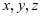 是具有轮换对称性,其实大家观察四个一阶导数会发现,“三胞胎”应该是
是具有轮换对称性,其实大家观察四个一阶导数会发现,“三胞胎”应该是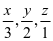 ,因此结果才是6,4,2的关系,而不是4,4,4。这里留下这样一个问题仅供思考,为什么满足轮换对称的不是
,因此结果才是6,4,2的关系,而不是4,4,4。这里留下这样一个问题仅供思考,为什么满足轮换对称的不是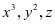 呢。
呢。
3.3 简化重积分和曲线曲面积分运算
在重积分和曲线曲面积分中,轮换对称性的用法比较简单。我们以二重积分为例:若积分区域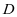 关于
关于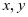 具有轮换对称性,则
具有轮换对称性,则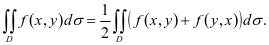
例3 计算二重积分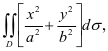 其中
其中
解 由于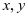 是双胞胎,因此
是双胞胎,因此

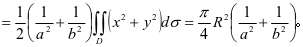
例4 求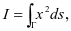 其中
其中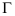 是圆周
是圆周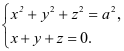
解 所求被积函数中只有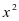 项,而轮换对称是三胞胎存在的,因此
项,而轮换对称是三胞胎存在的,因此
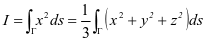
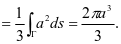
例5 计算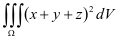 ,其中
,其中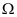 是由抛物面
是由抛物面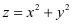 和球面
和球面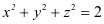 所围成的空间闭区域。
所围成的空间闭区域。
解 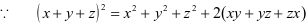 ,其中
,其中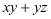 是关于
是关于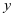 的奇函数,且
的奇函数,且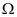 关于
关于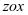 面对称,
面对称,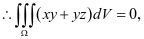
同理  是关于
是关于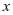 的奇函数,且
的奇函数,且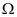 关于
关于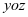 面对称,
面对称,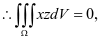
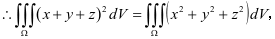
注意:该处具有轮换对称性的变量只有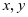 两个,而不是三个变量。因此
两个,而不是三个变量。因此
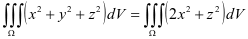
接下来的计算就没有问题了,第一部分用柱面坐标法,第二部分可以用截面法或柱面坐标法,此处不再累述。
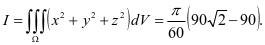
小结
本文抛砖引玉,简单将轮换对称性进行了简单总结,需要注意的是,在使用轮换对称简化运算过程中,一定要认清具有轮换对称的变量个数,是部分还是全部,这个将直接影响后续的运算。
参考文献:
[1]纪铭,杜朝丽.对称性在二重积分中的应用[J].东方教育.2017.09
[2]同济大学应用数学系.高等数学(下)[M].北京:高等教育出版社,2016